Just for fun, I followed along this tutorial on how to build LeNet – an early & famously successful neural net used for handwriting recognition – in Python. I’ve been playing with the data a bit to see how my modifications affect the learning rate. Here’s what I tried:
- Rotate each image by 90deg
- Rotate each image by 180deg
- Rotate each image by 270deg
- Invert high and low values (Note: high values are represented by white and low values are represented by black)
- Fade image – reduce intensity by halving all values
- Eliminate “in-between” values – all pixel values are either 1 (white) or 0 (black)
- Randomly rotate each image (by either 90, 180 or 270deg)
- Randomly rotate each image, after adding an indicator line to the bottom of the image
Uniform Rotation
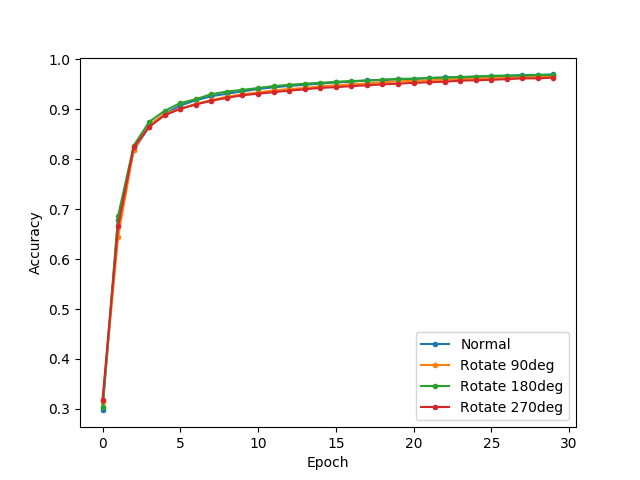
To begin with, I rotated the images by, in turn, 90, 180, and 270 degrees.
...
data = dataset.data.reshape((dataset.data.shape[0], 28, 28))
rotation = 1 # 90deg
# rotation = 2 # 180deg
# rotation = 3 # 270deg
for i, val in enumerate(data):
data[i] = np.rot90(data[i], rotation)
...
At each rotation, I ran LeNet for 30 epochs. As expected, those transformations did not appear to affect learning rate, because the transformation was applied uniformly across all data. In addition, these transformations will not affect any other attributes of the data, such as mean value over the whole image.
Value/Intensity
I then tried playing around with the values in the image.
...
def transformData(data):
return data/255. # normal (values must, in any case, be converted from range 0-255 to range 0-1)
# return 1 - (data/255.) # invert values
# return data/(255. * 2) # fade image - reduce intensity by halving all values
# return data > 127.5 # make values binary
(trainData, testData, trainLabels, testLabels) = train_test_split(
transformData(data), dataset.target.astype("int"), test_size=0.33)
...
As in the case of uniform rotation across all data, these changes were applied uniformly to all data. So, we wouldn’t expect these alterations to have a substantial negative impact on the ability of the network to eventually converge. However, these alteration will have changed important underlying structures of the data such as the mean and variance of the values in any given image. To illustrate, applying these value/intensity transformations to one set of 5 randomly chosen images results in the following:
normal
------
mean: 0.119206682497
variance: 0.0883226659517
binary
------
mean: 0.123979591837
variance: 0.108608652645
fade
----
mean: 0.0596033412487
variance: 0.0220806664879
invert
------
mean: 0.880793317503
variance: 0.0883226659517
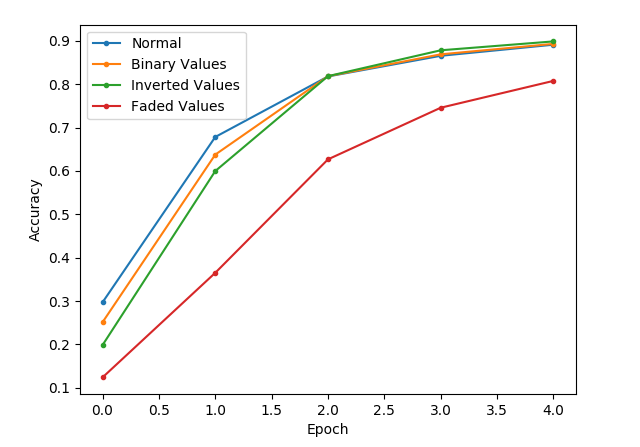
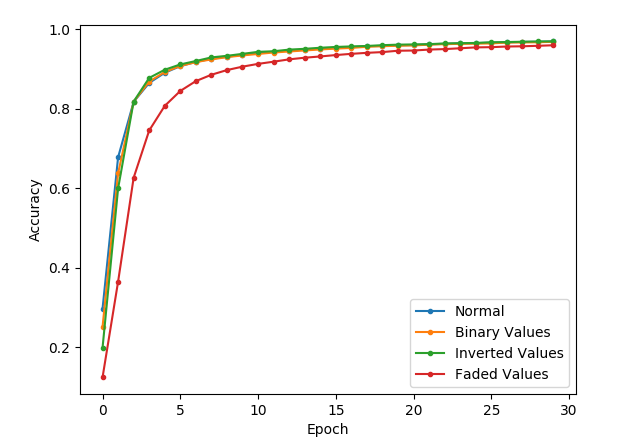
As you can see below, the binary color and inverted color images get off to a slower start but soon catch up, after 5 epochs.
The faded image, however, also gets off to a slow start but takes many more epochs to catch up.
Random Rotation
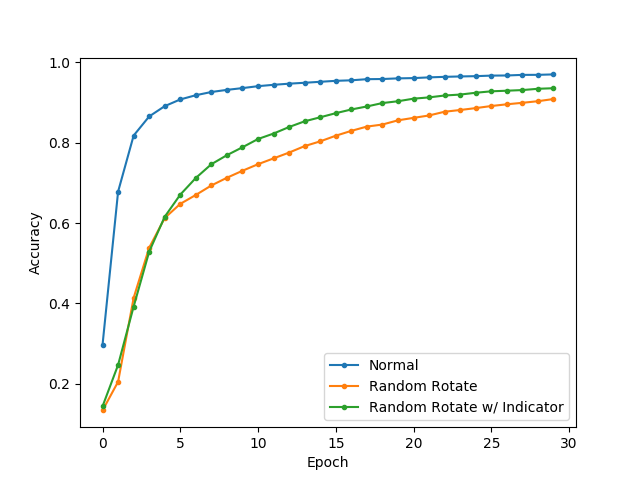
Finally, I randomly rotated the images, both with and without the addition of an “indicator” line (a line of all 1s – pure white – added to the bottom of the image before applying the random rotation, to serve as an indicator of the “true” bottom of the image:
...
data = dataset.data.reshape((dataset.data.shape[0], 28, 28))
for i, val in enumerate(data):
indicator = np.ones(28) * 255.
# data[i][27] = indicator.tolist() # add indicator
data[i] = np.rot90(data[i], randint(0,3))
...
Unsurprisingly, the worst performance of all the data modifications occurred as a result of randomly rotating the images. In this case, the transformation was not uniformly applied to each image. The addition of the indicator line had a substantial positive impact on the learning rate. However, interestingly, this positive effect was only observed after 5 epochs. Even so, neither modification was able to eventually converge to an accuracy similar to unmodified data, after 30 epochs.